"Please see my WPP13-14, made in collaboration with Jesus H., by visiting his blog jesushperiod5.blogspot.com. Also be sure to check out the other awesome posts on his blog."
Tuesday, March 18, 2014
Sunday, March 16, 2014
BQ#1: Unit P Concept 1 and 4 Law of Sines and the Area of an Oblique Triangle
i. Law of Sines
Why do we need it?
Well, in the past we have been working with all right triangles and it was rather easy when we had to find an angle or a side length due to the fact that we would use SOH CAH TOA (Sine, Cosine, or Tangent), or we would use the Pythagorean Theorem (a^2+b^2=c^2). However, what do we do when it comes to non-right triangles? Hmm..well the law of sines isn't just there for no reason. We can use the Law of Sines to figure out what an angle or side off a triangle is. The law of sines formula is the following:
http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif
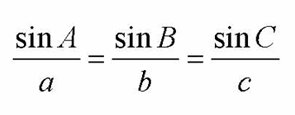
http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpg
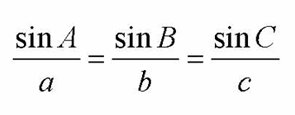
http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpg
How is it derived?
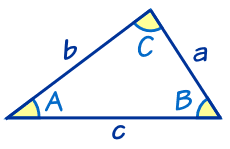
Okay so having a regular triangle in front of us, we would draw a vertical line form angle C down to the side length ab making two triangles now and we can label that with an "h" since it is the height. The height will belong to both triangles and a right triangle will be made. Yay! Right triangles are easier to work with right? The bottom picture will give you a visual so you can see how it's done and for further help.
http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif
Now, we know that the formula for the area of a triangle is A= 1/2 Base x Height, yet we can change it up depending on what we are looking for and it can still mean the same thing. That's the beauty of math! So, if we are trying to find h and we know that sinA= h/c and in order to find h we can say h= csinA by simply multiplying c to both sides. Same as if we were using sinC, sinC=h/a and in order to find h we would multiply a to both sides and we would end with a result looking like this, h=asinC. It does become a bit easier now because we are aware that these expressions are both equaled to h so can we not just equal them to each other? Yes! Therefore, we would have csinA=asinC. Are we done? No because well the formula doesn't look it should as stated above. One more step! To get sinA and sinC alone on the top we will divide by ac and then we would have SinA/a=SinC/c. You might ask yourself what about the B, but in reality it is the same thing. If we would have used angle B instead of C we should have SinA/a=SinB/b. We can see that they are all equal to each other and so the order does not matter. And that is how the formula is as is and came to be. The following images will help a bit more and you shall see what is going on.
iv. Area Formula (Oblique Formula)
In order to find the area of a triangle we use the formula A=1/2bh and this would certainly work out if all triangles were right triangles, but since life isn't always nice and sweet we will get triangles of which are not right and we have to be able to find h, the height.
We would begin by doing the same thing as before and cutting the triangle into two by drawing the vertical line. Since we do not know what h is what can we do? Well, we do know that h=aSinC like we discovered up above first, so we can substitute. A=1/2b(aSinC). Now, we can use more than one depending on what angles and stuff. For example we could use 1/2 bc SinA; 1/2 ac SinB; 1/2 ab SinC.
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp
References:
http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif
http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpghttps://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp
Wednesday, March 5, 2014
WPP #12: Unit O Concept 10: Solving angles of elevation and depression word problems
A) Sophia is tired of the same routine and so she decides to go up to the mountains with Edward and more friends. She is excited and thrilled about the whole trip up to Big Bear and she is hoping to have a blast with everyone. Now, as soon as they get there, Edward suggests going skiing and everyone says yes. As Sophia gets ready and then puts her skis on at the bottom of the mountain, she stands 700 feet away from it, she finds that the angle of elevation is 15 degrees. Before actually going up the mountain and then having a blast coming down, Sophia wants to know how high the mountain is. Estimate the height of the mountain and round to the nearest foot.
B) So, after a while Sophie and Edward were the first ones to make it to the top of the mountain and they decide to contemplate the view from up top and they enjoy themselves for a while before racing down. As Sophia gets ready to ski down she stands at the tip of it and looks down. She estimates the angle of depression to be 25 degrees from where she is at the top to the very bottom of the mountain where all of her other friends were. Also, she is aware that the height of which she is found in now is 850 feet. How far down is the path that she will ski down? Round to the nearest foot.
Answers:
Cites for the 2 pictures I got on Google:
http://www.disneyclips.com/imagesnewb/imageslwrakr01/pooh_tigger_piglet_eeyore_skis.gif
https://www.google.com/search?tbm=isch&tbs=simg:CAQSWxpZCxCo1NgEGgIICQwLELCMpwgaMgowCAESCqQEqQSsBKMEqAQaIKKoJxY7wJjGpCP8yYxW5LjlhGuMA5uFdfg5i9pv13V4DAsQjq7-CBoKCggIARIEasBVogw&sa=X&ei=vQ4YU7z2MZL9oATJm4EQ&ved=0CCMQwg4oAA&biw=1366&bih=667#facrc=_&imgdii=_&imgrc=rmBk_ghzxFEHvM%253A%3BAjyJcOxxAv9kwM%3Bhttp%253A%252F%252Fimg1.etsystatic.com%252F024%252F0%252F8427078%252Fil_340x270.490026831_a8ds.jpg%3Bhttp%253A%252F%252Fwww.etsy.com%252Fmarket%252Ffrozen_lake%3B340%3B270
Monday, March 3, 2014
I/D #2: Unit O Concept 7-8: Deriving the patterns for the 45-45-90 and 30-60-90 Triangles
Inquiry Activity Summary:
Today in class we were given a square and an equilateral triangle both having a side length of 1 and we were to explain the thought process step by step in order to be able and literally know how and why the special right triangles have their constants and basically where they come from. Now, for the 45-45-90 triangle we were given the square that had a length of 1 while for the 30-60-90 triangle we were given the equilateral triangle with a length of 1 and from there we were to completely derive it and see how you get n, n, n radical 2 for the 45 degree one and n, n radical 3, and 2n. Okay so although it seems like we know nothing and we feel like we cannot figure out..we can step by step.
1. Okay so beginning with the square that we were given for the 45 degree special triangle, we can automatically label all four sides with a 1 since we know that a square is all equal in sides and the directions did say that the square contained a side length of 1. Now, we can bisect the square diagonally of course because if we did it vertically it will not create a triangle, but a rectangle. Then, it only gets easier and this is why, we know that two sides are equaled to 1 and so in order to find the third side we can use the wonderful ...PYTHAGOREAN THEOREM! After solving it by using a^2+b^2=c^2 we should get c= radical 2. Okay now I know what you are thinking well then where does the n come from and well truth is n is just used as a constant it really isn't anything else but a constant/variable like x could be. So we could label all three sides of the right triangle as n like any variable and then we find that the sides conclude to being n, n, and n radical 2. The reason we use n is to that we can see the relationship with all sides and so we can see the possible numbers that could be interchangeable. There is a visual below so that it can be easier in understanding and seeing a picture may clear confusions.
2. Okay so now for the 30-60-90 triangle we are given an equilateral triangle of which we all know has three angles that are 60 degrees. We can begin by labeling the three sides with one since the directions as well told us that there was a side length equal to 1. In order to have it become a right triangle we simply bisect it vertically and the reason is considering that we will get a 90 degree, a 30, and a 60 degree like shown below. By cutting it so, it basically creates out special triangle with the wanted angles. Now, by just focusing on the triangle we want we can see that the bottom becomes 1/2 after bisecting it, while the hypotenuse still is 1, and now what about the height? Well, we can use the Pythagorean Theorem again and after plugging in and solving, we should get b= radical 3/2. Okay so now we have 1, radical 3/2, and 1/2, yet we are not done. After, we can do some more solving by multiplying by 2. This is so because well 1/2 times 2 gives us one and that is what we originally had, yet now we have to do it to all sides. Next, once we multiply we should get 2 for the hypotenuse, 1 for the bottom horizontal line and lastly radical 3 for the height. Now, almost finishing, where the heck does the n mean and why does it fit in? Well, n is just a constant of which we use to compare the sides and it basically represents the different number values. Now, after we label all sides with the n as simply a variable we end up getting n, n radical 3, and 2n. The figures below help much visually when it comes to understanding.
Today in class we were given a square and an equilateral triangle both having a side length of 1 and we were to explain the thought process step by step in order to be able and literally know how and why the special right triangles have their constants and basically where they come from. Now, for the 45-45-90 triangle we were given the square that had a length of 1 while for the 30-60-90 triangle we were given the equilateral triangle with a length of 1 and from there we were to completely derive it and see how you get n, n, n radical 2 for the 45 degree one and n, n radical 3, and 2n. Okay so although it seems like we know nothing and we feel like we cannot figure out..we can step by step.
1. Okay so beginning with the square that we were given for the 45 degree special triangle, we can automatically label all four sides with a 1 since we know that a square is all equal in sides and the directions did say that the square contained a side length of 1. Now, we can bisect the square diagonally of course because if we did it vertically it will not create a triangle, but a rectangle. Then, it only gets easier and this is why, we know that two sides are equaled to 1 and so in order to find the third side we can use the wonderful ...PYTHAGOREAN THEOREM! After solving it by using a^2+b^2=c^2 we should get c= radical 2. Okay now I know what you are thinking well then where does the n come from and well truth is n is just used as a constant it really isn't anything else but a constant/variable like x could be. So we could label all three sides of the right triangle as n like any variable and then we find that the sides conclude to being n, n, and n radical 2. The reason we use n is to that we can see the relationship with all sides and so we can see the possible numbers that could be interchangeable. There is a visual below so that it can be easier in understanding and seeing a picture may clear confusions.
2. Okay so now for the 30-60-90 triangle we are given an equilateral triangle of which we all know has three angles that are 60 degrees. We can begin by labeling the three sides with one since the directions as well told us that there was a side length equal to 1. In order to have it become a right triangle we simply bisect it vertically and the reason is considering that we will get a 90 degree, a 30, and a 60 degree like shown below. By cutting it so, it basically creates out special triangle with the wanted angles. Now, by just focusing on the triangle we want we can see that the bottom becomes 1/2 after bisecting it, while the hypotenuse still is 1, and now what about the height? Well, we can use the Pythagorean Theorem again and after plugging in and solving, we should get b= radical 3/2. Okay so now we have 1, radical 3/2, and 1/2, yet we are not done. After, we can do some more solving by multiplying by 2. This is so because well 1/2 times 2 gives us one and that is what we originally had, yet now we have to do it to all sides. Next, once we multiply we should get 2 for the hypotenuse, 1 for the bottom horizontal line and lastly radical 3 for the height. Now, almost finishing, where the heck does the n mean and why does it fit in? Well, n is just a constant of which we use to compare the sides and it basically represents the different number values. Now, after we label all sides with the n as simply a variable we end up getting n, n radical 3, and 2n. The figures below help much visually when it comes to understanding.
Inquiry Activity Reflection:
1. "Something I never noticed before about special right triangles is that they can appear and simply pop out of no where and especially out of other shapes."
2. "Being able to derive these patterns myself aids in my learning because I can actually see what I am learning and exactly where this comes from that this didn't just appear form thin air."
Saturday, February 22, 2014
I/D#1:Unit N Concept 7: How do RST relate to the UC?
Inquiry Activity Summary:
1. 30 degrees
Several different instructions were given in order to complete this special right triangle of 30 degrees and much labeling in order to understand. To start with, the three sides of the triangle had to be labeled for their identification. So, one thing we know for sure and that is that our hypotenuse is equaled to 1 considering that these triangles all come from within a unit circle and what is a unit circle? Well a unit circle is one of which has a radius of one and therefore, we can see how the longer side (hypotenuse) is that radius of the circle. Now, according to the special rules of right triangles we know that the side adjacent to the 30 degrees (form the picture it is the horizontal side labeled x) will be n radical 3. Also, we find out that the side opposite from the 30 degrees (due to the picture it is the vertical side labeled y) will be n and finally we get to the hypotenuse (r) of which is said to be 2n. Okay now that that is over with, we can actually find real number values and that is done by using two trig functions: Sine and Cosine. Sine of 30 degrees is done by using SOH and therefore will be opposite over hypotenuse; we can write it out as y/r or x/2x of which equals 1/2 once it is simplified. Doing the same thing with cosine but this time using CAH, adjacent over hypotenuse, it would be x/r and with the variables it would be radical 3/2 after the simplifying like shown in the image above. If we were to treat the triangle on a coordinate plane with the origin of the 30 degrees being (0,0) then the corner as you move horizontally will be (radical 3/2,0) and lastly, the point at the highest tip will be (radical 3/2, 1/2).
2. 45 degrees
Now the same types of instructions apply to this 45 degree triangle, yet the numbers will be different. Okay so to start we can label the adjacent side, the horizontal side of the given angle on the left hand corner x. The opposite side of the angle or the vertical side will be labeled as y and lastly for now the hypotenuse will be r=1. To label according to STR, both x and y will be n, and as for the hypotenuse is will be n radical 2 after simplifying of course like shown in the image. The trig functions world the same as last time with sine and cosine. Sine and cosine are actually the same number values and they both include the same type of simplification since for both the x and y it is n/n radical 2 of which reduces to radical 2 over 2. From my perspective this special triangle is the easiest and includes less work. Picturing the image on a coordinate plane, the origin will be (0,0) and as you move horizontally across then the next point will be (radical 2/2, 0) and then as for the last vertical tip point it will be (radical 2/2, radical 2/2).
3. 60 degrees
Okay so we are finally looking at the last type of triangle! Yay! We shall label the horizontal and vertical and hypotenuse like the same as the others, with x, y, and r=1. X is the adjacent and y is the opposite one. Considering the special rules, x will be n and y will be n radical 3. To find sine of 60 degrees then it will be y/r and then to find actual values it will turn into radical 3 over 2. Also, for cosine it will be x/r and then 1/2 after the simplification as shown. Treating the triangle as if on a coordinate plane starting as the origin (0,0) and then as you keep going across horizontally the point will become (1/2,0). Lastly, the last point will be (1/2,radical 3/2).
4. This activity helps derive the unit circle by being able to see special right triangles from within the circle. We can see how the SOH CAH TOA can develop and we can see the different types of degrees within it.
5.
1. 30 degrees
Several different instructions were given in order to complete this special right triangle of 30 degrees and much labeling in order to understand. To start with, the three sides of the triangle had to be labeled for their identification. So, one thing we know for sure and that is that our hypotenuse is equaled to 1 considering that these triangles all come from within a unit circle and what is a unit circle? Well a unit circle is one of which has a radius of one and therefore, we can see how the longer side (hypotenuse) is that radius of the circle. Now, according to the special rules of right triangles we know that the side adjacent to the 30 degrees (form the picture it is the horizontal side labeled x) will be n radical 3. Also, we find out that the side opposite from the 30 degrees (due to the picture it is the vertical side labeled y) will be n and finally we get to the hypotenuse (r) of which is said to be 2n. Okay now that that is over with, we can actually find real number values and that is done by using two trig functions: Sine and Cosine. Sine of 30 degrees is done by using SOH and therefore will be opposite over hypotenuse; we can write it out as y/r or x/2x of which equals 1/2 once it is simplified. Doing the same thing with cosine but this time using CAH, adjacent over hypotenuse, it would be x/r and with the variables it would be radical 3/2 after the simplifying like shown in the image above. If we were to treat the triangle on a coordinate plane with the origin of the 30 degrees being (0,0) then the corner as you move horizontally will be (radical 3/2,0) and lastly, the point at the highest tip will be (radical 3/2, 1/2).
2. 45 degrees
Now the same types of instructions apply to this 45 degree triangle, yet the numbers will be different. Okay so to start we can label the adjacent side, the horizontal side of the given angle on the left hand corner x. The opposite side of the angle or the vertical side will be labeled as y and lastly for now the hypotenuse will be r=1. To label according to STR, both x and y will be n, and as for the hypotenuse is will be n radical 2 after simplifying of course like shown in the image. The trig functions world the same as last time with sine and cosine. Sine and cosine are actually the same number values and they both include the same type of simplification since for both the x and y it is n/n radical 2 of which reduces to radical 2 over 2. From my perspective this special triangle is the easiest and includes less work. Picturing the image on a coordinate plane, the origin will be (0,0) and as you move horizontally across then the next point will be (radical 2/2, 0) and then as for the last vertical tip point it will be (radical 2/2, radical 2/2).
3. 60 degrees
Okay so we are finally looking at the last type of triangle! Yay! We shall label the horizontal and vertical and hypotenuse like the same as the others, with x, y, and r=1. X is the adjacent and y is the opposite one. Considering the special rules, x will be n and y will be n radical 3. To find sine of 60 degrees then it will be y/r and then to find actual values it will turn into radical 3 over 2. Also, for cosine it will be x/r and then 1/2 after the simplification as shown. Treating the triangle as if on a coordinate plane starting as the origin (0,0) and then as you keep going across horizontally the point will become (1/2,0). Lastly, the last point will be (1/2,radical 3/2).
4. This activity helps derive the unit circle by being able to see special right triangles from within the circle. We can see how the SOH CAH TOA can develop and we can see the different types of degrees within it.
5.
 |
Depending on which quadrant the SRT is found, that will be the determination on whether it will be positive or negative. If it will be found on quadrant one then both x and y will be positive; if it is then in quadrant 2 then only the x value will be negative while the y is positive. Also, the third quadrant both x and y are negative. Lastly, for quadrant 4 then only the y value is negative.
1. The coolest thing I have learned from this activity was...that the unit circle actually does include the special right triangles and how a lot can come from a simple circle.
2. This activity will help me in this unit because ... I will not have to literally memorize the entire unit circle.
3. Something I never realized before about special right triangles and the unit circle is... how they can come together and actually make sense. I would've never thought so much could be learned.
|
Monday, February 10, 2014
RWA #1: Unit M Concept 5: Ellipses
1. Definition: the set of all points such that the sum of the distance from 2 points, known as the foci, is a constant.
2. Properties: The equation of an ellipse looks like this and it has a bit more information below:
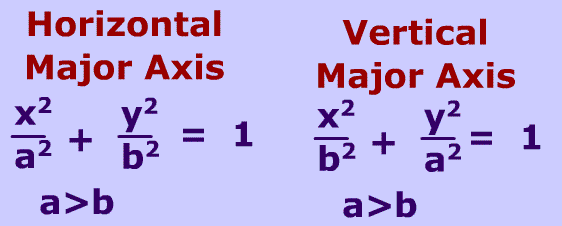
3. The Real World Application:
The solar system is an example of ellipses. They discovered that the planets travel around the sun from one of its foci. To see the example and actually view and have this real world application explained then view the video below.
4. The Works Cited
http://www.youtube.com/watch?v=48tXquj94w8
http://www.purplemath.com/modules/ellipse.htm
http://www.youtube.com/watch?v=9xSgKqTxZbg
https://www.google.com/search?hl=en&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=ellipse+equation&oq=ellipse+&gs_l=img.3.0.0l10.8705.9953.0.14344.8.8.0.0.0.0.110.724.3j5.8.0....0...1ac.1.34.img..1.7.620.M5FepgyTgVw#hl=en&q=horizontal+and+vertical+ellipsis&spell=1&tbm=isch&imgdii=_
https://www.google.com/search?hl=en&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=ellipse+equation&oq=ellipse+&gs_l=img.3.0.0l10.8705.9953.0.14344.8.8.0.0.0.0.110.724.3j5.8.0....0...1ac.1.34.img..1.7.620.M5FepgyTgVw#hl=en&q=ellipses+equation&tbm=isch&facrc=_&imgdii=_&imgrc=FBWW2sN-ezU7hM%253A%3BIgSAy7XveaBvgM%3Bhttp%253A%252F%252Fwww.descarta2d.com%252FBookHTML%252FChapters%252FHTMLFiles%252Fell_32.gif%3Bhttp%253A%252F%252Fwww.descarta2d.com%252FBookHTML%252FChapters%252Fell.html%3B346%3B233
2. Properties: The equation of an ellipse looks like this and it has a bit more information below:
To describe it graphically, an ellipse has a sort of oval type shape and it can either be skinny or a fat one. The ellipse has a major and a minor axis, followed by a center and then there is also a foci of which lies inside within the ellipse. The following image shows an example of a horizontal and vertical ellipse:
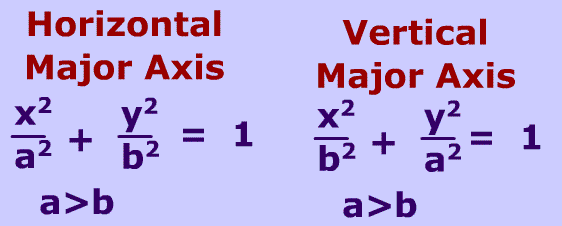
For more information on ellipses go to: http://www.purplemath.com/modules/ellipse.htm
All of the features of an ellipse involve the center of which is made up of (h,k) and then finding the vertices and the co-vertices. Now, to do so you take the square root of the value of a and then adding or subtracting it to the h or k depending on whether it's major axis is vertical or horizontal. The co-vertices you can find likewise just that you would use b and then add or subtract. The foci comes in next and it dictates where the foci is going to be and it tells whether the ellipse will be horizontal or vertical. Lastly, for the eccentricity of the ellipse, it will always be greater than 0 but less than one. Below will be a video of which will tell how you can solve an ellipse and it contains extra help on the graphing as well:
3. The Real World Application:
The solar system is an example of ellipses. They discovered that the planets travel around the sun from one of its foci. To see the example and actually view and have this real world application explained then view the video below.
4. The Works Cited
http://www.youtube.com/watch?v=48tXquj94w8
http://www.purplemath.com/modules/ellipse.htm
http://www.youtube.com/watch?v=9xSgKqTxZbg
https://www.google.com/search?hl=en&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=ellipse+equation&oq=ellipse+&gs_l=img.3.0.0l10.8705.9953.0.14344.8.8.0.0.0.0.110.724.3j5.8.0....0...1ac.1.34.img..1.7.620.M5FepgyTgVw#hl=en&q=horizontal+and+vertical+ellipsis&spell=1&tbm=isch&imgdii=_
https://www.google.com/search?hl=en&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=ellipse+equation&oq=ellipse+&gs_l=img.3.0.0l10.8705.9953.0.14344.8.8.0.0.0.0.110.724.3j5.8.0....0...1ac.1.34.img..1.7.620.M5FepgyTgVw#hl=en&q=ellipses+equation&tbm=isch&facrc=_&imgdii=_&imgrc=FBWW2sN-ezU7hM%253A%3BIgSAy7XveaBvgM%3Bhttp%253A%252F%252Fwww.descarta2d.com%252FBookHTML%252FChapters%252FHTMLFiles%252Fell_32.gif%3Bhttp%253A%252F%252Fwww.descarta2d.com%252FBookHTML%252FChapters%252Fell.html%3B346%3B233
Thursday, December 19, 2013
Subscribe to:
Posts (Atom)