BQ#7: Unit V: Deriving the Difference Quotient

Deriving the difference quotient? ..What? ...Well, si se puede!

So, first of all let's recall the difference quotient formula and remember what it has in the entire thing. 

(http://www.coolmath.com/algebra/15-functions/images/08-functions-01.gif)

Remember the song for it? Yes! It is said like this: "f of x plus h, minus f of x, divided by the letter h that's the difference quotient!" (in rhythm) 

If we take a simple, regular (x,y) graph that we are familiar with, it can be somewhat easier to  understand..to begin with. Now, like the picture below, we have a point there and instead of being 1 or 5 like a scale we would normally see, we can just call it 'x'. Then, that means that the y value would have to be f(x). If you find it confusing then think of it with numbers to make sense out of it. If we had 1 instead of x, then the y value would have to be f(1) or even if we had 5 as the x value, then the y would be f((5). Making more sense? Hopefully, so now we can continue. Like shown below, if we had the next measurement it would be x+h and the reasoning is this: if we say that the distance from x, the first point, to the second point is of h value, then our second x point would be x+h. That means that the y-value for x+h would be f(x+h). 

Almost finishing up, we would have to use the slope formula in order to continue and the formula is: 

(http://0.tqn.com/d/create/1/0/9/p/C/-/slopeformula.jpg)

The derivative is basically slope and when we are looking for the derivative, then that just means we are looking for the slope of the horizontal tangent/secant line. The two coordinates that we found we can use to plug in to the slope formula. The visual is in the image below. Okay lastly, we should clear up what in the world is a tangent and a secant line? Well, a secant line is one of which touches the graph at two point while tangent lines touch the graph at one point only. 

Still need more help and I spoke gibberish, then go ahead and watch the video below:

            (https://www.youtube.com/watch?v=XA0fZh8cXV8)

References:

(http://www.coolmath.com/algebra/15-functions/images/08-functions-01.gif)

(http://0.tqn.com/d/create/1/0/9/p/C/-/slopeformula.jpg)

(https://www.youtube.com/watch?v=XA0fZh8cXV8)

BQ #6: Unit U

1. What is continuity? What is discontinuity?

Continuity basically means that the graph will be predictable, it will have NO breaks, NO jumps, and NO holes, it can be drawn without lifting your pencil, and lastly, the value (actual height) and the limit (intended height) will be the same. In other words what this means is that the graph will go where you think it will go and nothing will be there to interrupt the graph, so no holes, jumps, etc. For example, the picture below.

                                                     (http://www.conservapedia.com/images/2/2f/Br-cont-function.png)

Okay, so now what about a discontinuity? Well a discontinuity will have to be where a function is NOT continuous meaning that it will have breaks, jumps, holes, it will not be predictable, and the limit and the value of the graph will not be the same and equal to each other. We are aware that there are two types of families for the functions that would be removable and non-removable. There is only one removable function and that is the point (hole) discontinuity. The point discontinuity is the only on that has limit as well while the three that we non-removable do not have a limit, or said properly, the limit does not exist at the non-removable discontinuities. These non-removable are jump discontinuity, oscillating behavior, and infinite behavior. Now, the reason that the limit does not exist is due to the fact that in a jump there is a different left and right and the do not meet, in oscillating behavior,...well that thing is just going up and down and it is just confused, and lastly, the infinite behavior means that there is a vertical asymptote which leads to unbounded behavior and also, infinity is not a real number to be dealing with.

This image is an example of a point (hole) discontinuity:

                                        (http://faculty.wlc.edu/buelow/common/imageN20.JPG)

This image is an example of a jump discontinuity:

(http://image.tutorvista.com/content/feed/u364/discontin.GIF)

This image is an example of oscillating behavior:

(http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg)

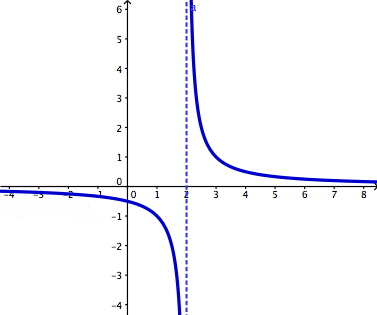
This image is an example of infinite discontinuity:

(http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif)

2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is the INTENDED height of a function. A limit exists only when the left side and the right side of the graph meet. Sometimes the circle on the graph is not shaded in and it an open circle, so take a point discontinuity..that's a perfect example because a limit still exist at the point since a limit is only the INTENDED value and that is where the graph is intending to go. Now, at the other three discontinuities the limits do not exist and that is because for some reason the left and right do not match and meet, there is oscillating behavior, and/or there is infinite behavior. The main difference between a limit and a value is that the limit is the INTENDED height of a function, while a value is the ACTUAL height of a function.

3. How do we evaluate limits numerically, graphically, and algebraically?

To evaluate the limit numerically, you would take a t-table of x and y values. We begin by putting the number they give us that it is approaching in the middle of the table and then fill the left and right with the closest numbers that head to the one in the middle. That is actually the most confusing and most difficult because then you can just take your calculator and plug in the numbers to be able to hit trace and basically then just copy down the numbers. For example:


(http://archives.math.utk.edu/ICTCM/VOL10/C006/image2.gif)

To evaluate the limit graphically, we simply put a finger on the left and a finger on the right and follow the graph until your fingers meet ...well...if they meet. Remember they will not always meet because it can be a jump, etc. For example take the graph below and see how if you trace the graph your fingers will not meet because it is a jump and they are different values...this is not like a point of which your fingers would meet.

(http://www.vitutor.com/calculus/limits/images/0_268.gif)

Lastly, to evaluate a limit algebraically, is well you are using equations and we solve. The methods we can use are direct substitution, dividing out/factoring method, and the rationalizing/conjugate method.

Works Cited:
http://www.conservapedia.com/images/2/2f/Br-cont-function.png

http://faculty.wlc.edu/buelow/common/imageN20.JPG

http://image.tutorvista.com/content/feed/u364/discontin.GIF

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif

http://archives.math.utk.edu/ICTCM/VOL10/C006/image2.gi

http://www.vitutor.com/calculus/limits/images/0_268.gif

BQ#3: Unit T Concepts 1-3: Trig Graphs

How do the graphs of sine and cosine relate to each of the others? Emphasize asymptotes in your response. 
-Tangent
-Cotangent
-Secant
-Cosecant 

1) Tangent 
     Okay so the ratio identity for tangent we know is sine/cosine. Also, we are aware that we will only have asymptotes where we get an undefined answer meaning that we divide by zero and therefore, cosine would have to be zero in order to make this asymptotes and an undefined answer. Now, we will have asymptotes at the 90 and 270 degree, so at pi/2 and 3pi/2. This being said, we know that tangent cannot touch them no matter what. Now, there are way more asymptotes, they practically go on forever, yet we can just stick to some.

2) Cotangent 
        We can basically use the same knowledge from above with Tangent, yet now we know that cotangent is equaled to cosine over sine and so the asymptotes will be found where cosine is zero so at 90 and 270 degrees, or pi/2 and 3pi/2. And we remember that the graph cannot touch the asymptotes!

3) Secant 

      We know that secant is the reciprocal of cosine and the ratio is 1/cos. Secant as well has asymptotes that are found where cosine is equaled to zero as well. 

4) Cosecant 

      Now, the same rules apply like with the reciprocals and stuff yet the asymptotes will be located in different places due to the different kind of graph. Cosecant is the reciprocal of sine so its ratio is 1/sin. 

References:

http://mathsm1m0838.edublogs.org/files/2009/08/Picture-11.png

http://2.bp.blogspot.com/-KGMdRWBNlP8/UXi7SKh2BjI/AAAAAAAAAEU/YSex9MpWZAk/s640/2013-04-24+22.05.53-1.jpg

http://www.mathipedia.com/GraphingSecant,Cosecant,andCotangent_files/image014.jpg

http://www.ask-math.com/images/Cosecantgraph.png

BQ#4: Unit T Concept 3: Tangent and Cotangent Graphs

Why is the "normal" tangent graph uphill, but a "normal" cotangent graph downhill? Use unit circle ratios to explain.
        
        The reason that a tangent graph is uphill and yet a cotangent graph is downhill is due to the fact that they are different ratios and different of which then creates different asymptotes. We know that tan=sin/cos and cot=cos/sin, or in other words, tan is equaled to y/x and cot is equaled to x/y. See how the denominators are different, tangent has a denominator of cosine while cotangent has a denominator of sine and therefore for tangent we would get our asymptotes wherever cosine is equaled to zero which would be at the 90 degree (pi/2) and at the 270 degree (3pi/2). Furthermore, for cotangent we would get asymptotes wherever sine is equaled to zero which would be at the 0 degree (0) and at the 180 degree (pi). We do know that the pattern for both is positive, negative, positive, negative, yet the asymptotes are located in distinct places and so creates a different looking graph.   

References:

-http://www.mathamazement.com/images/Pre-Calculus/04_Trigonometric-Functions/04_06_Graphs-of-Other-Trig-Functions/cotangent-graph.JPG

-http://www.regentsprep.org/Regents/math/algtrig/ATT7/otherg91.gif

BQ#5: Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain. 
     The reason that sine and cosine cannot have asymptotes is due to the fact that they will never be undefined. Now, let's recall that in order for there to any asymptotes then we have to have an answer as undefined. Okay, with that in mind we can now prove that sine and cosine do NOT have any asymptotes. We know that the ratio for sine is y over r and as for cosine, we know that it is x over r. "R" is always equaled to one right? And since we will never have a zero be on the denominator, then that means that no asymptotes will be present and created. 
      
     The other four trig graphs do have asymptotes and that is because they will not ever have r or a 1 as the denominator. For example, if we did tangent, then we know the ratio is sine (y) over cosine (x) and we know that x can be a zero at the 90 degrees and at the 270 degrees, or pi and 3pi over 2. Also for secant, it would be the same thing since the ratio is r over x and x can be a zero like stated before. Lastly, cosecant (r/y) and cotangent (x/y), they have a denominator of y and we know that y can be equaled to zero at 0 degrees and 180 degrees, or in other words, 0 and pi.  

BQ#2: Unit T Concept Intro: Trig Graphs and the Unit Circle

How do trig graphs relate to the Unit Circle?
   Okay so I know what you are thinking..the Unit Circle again?! Well yes, the Unit Circle comes in from everywhere and somehow has a function for everything. For trig graphs, it is as if you are seeing the Unit Circle, yet in a straight line and the same numbers are present in order. Also, their signs depend on what quadrant they are found in. For example, if we have cosine, we know that it is positive in quadrants 1 and 4.

1. Period? Why is the period for sine and cosine 2pi, whereas the period for the period for tangent and cotangent is pi?
    The period for sine and cosine is 2pi due to the pattern that it follows and how it repeats after every four marks on a graph. Now, for tangent and cotangent and we are able to see that it repeats every two marks. For proof we can see it after knowing that the symbols are positive, negative, positive, negative and so that means that it only takes two marks. 

2. Amplitude?-How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?
    So first of all, what are amplitudes? Well an amplitude is half the distance between the highest and lowest points on the graph. They can be found by looking at the value of |a|. Sine and cosine have the same amplitude of which is 1 and -1 due to the fact that they are the ones with the restrictions. They cannot be any points greater than or less than 1 and -1 since they don't exist anymore. Now, we get to tangent and cotangent. They have no restrictions and therefore can keep going on and on and on. Their range will always be negative infinity to positive infinity. Lastly, we have cosecant and secant of which simply don't have a range and therefore no amplitudes. 

Reflection#1: Unit Q: Verifying Trig Functions

Dear Future Math Students,

Unit Q deals with several fundamental identities, trig functions, ratios, and using different simplification processes in order to solve and verify as well. I know that this sounds like gibberish and that you probably want to cry because it just seems so confusing and you just do not want to go through this, but DON'T WORRY! I did it and it was okay....after you practice practice practice and get the feel for it. I am not going to lie, IT IS DIFFICULT! But it will not be the end of the world! Do not give up and try and practice and sooner or later you will succeed! (: Okay well let me go more in depth...


1. What does it actually mean to verify a trig identity?
-To verify simply means to check and prove that whatever is stated is true. For example, if you had 1+1=2 then you simply have to go through steps that will help you prove that 1+1 actually does equal 2. Of course, it will not be a nice and easy as my example. ...Sorry ._. And so, basically that you have to be sure to solve a problem and get the same answer as the one that is given and equaled to. Oh! and it is better when you have to verify rather than having to just solve and come up with an answer. The reason is that when you are verifying, you know the answer you should end up with and it is just you having to plug in and substitute and solve until you hit bingo and check the answer, whereas when it comes to just solving and you are obviously not given an answer, then you just have to solve correctly and pray you get it correct.

2. What tips and tricks have I found helpful?
-Okay so we know that there are a bunch of functions and ratios like sine, cosine, tangent, cosecant, secant, and cotangent, yet a tip I have is to turn everything into sin/cos at some point because it will become easier. Sine and cosine can be considered our best friends in this case. They are nice to us, so might as well use them. (; Also, I have foreseen the future and I know that you will feel discouraged and defeated, but NO! You can do this! DON'T GIVE UP! This is a tip that I know you WILL need! So use it! Keep working through it and take various adventures with the problem.

3. Explaining my thought process and steps I take in verifying a trig identity.
-Okay so if you noticed, I said that you should take various adventures with the problem and what did I mean? Well the beauty of these problems is that there isn't only one way on solving a problem so you really can't o wrong! Yay! If you begin differently than someone else, it's okay just keep going and don't get stuck, use your knowledge, you identities, your reciprocals. Now, when I encounter a problem I think and wonder what I should do first. Should I turn into sine and cosine? Should I multiply by the conjugate? Should I split the problem up maybe to see if something cancels? Or maybe I should find the least common denominator? Perhaps this is an identity? Honestly, I just think of what to do first and then I keep going just trying stuff and see where it takes me and I just use the skills I know. There is never one path so don't be afraid of trying something! (:

SP#7: Unit Q Concept 2: Finding all trig functions when given one trig function and quadrant (using identities)

"This SP#7 was made in collaboration with Tracey P. Please visit the other awesome posts on their blog by going here."

Now, there is more than one way to find our answers and solve for the function, two are those that will be expressed throughout this post. We know that we can solve this using identities or by using SOH CAH TOA! So, the following pictures will display the solutions to the problems in both ways and using both methods. (: In the end we will find out how you get the same answers either way!

The first image will show and go over how to solve this function when using identities.

This second image will go over solving the function by using the wonderful SOH CAH TOA!  

In order to be able and understand this problem and be able to deal with it as you solve it, you have to be able to know the different types of identities and they should be able to mix and match and substitute several terms for others. Also, of course you have to know what SOH CAH TOA is and the ratios for each. Also, you should be familiar with all of the ratios and how there could be more than one. It can be difficult, but with practice everything will be fine. (:  

I/D#3: Unit Q Concept 1: Pythagorean Identities

Inquiry Activity Summary:
1. Okay so we know that we are dealing with identities because the title is a given, yet what are identities? Well, an identity is basically any proven fact or formula of which brings the Pythagorean Theorem to mind considering that it is a formula that works and is always correct when put to use. Okay so let's start off with the Pythagorean Theorem. If we were given the terms x, y, and r then we would write out the formula like this: x^2+y^2=r^2, but we would tweak it a bit in order to have it equal to 1. We would divide by r^2, do we agree? Yes! Because that is pretty much the only way to equal an equation to 1, by dividing by whatever number the equation is equaled to. Then we would have (x/r)^2+(y/r)^2=1.
 
     Now, if we go back to the unit circle, oh yeah I forgot to mention that the unit circle does come back to haunt haha, we know that cosine is x/r or in other words, adjacent over hypotenuse and sine is y/r or opposite over hypotenuse, so ..do we see anything? Hmm.. Yea! It matches to much of the Pythagorean Theorem! We would just have to square the two variables on the left, x and y, and then equal them to 1. In the end we could have cos^2theta + sin^2theta= 1. Remember that cosine is x and sin is y so in reality we just do some switching around and have fun with it and therefore sin^2x+cos^2x=1 is referred to as a Pythagorean Identity. To prove the theory with some examples and so you can see it visually look at the images below if let's say we did the magic 45 degree.

2. Now, to derive the identity with Secant and Tangent we would start off with the original sin^2x+cos^2x=1. The first thing we would do is divide everything by cos^2x and we would get sin^2x/cos^2x + cos^2x/cos^2x= 1/cps^2x and we can still simplify this further! We know that sin^2x/cos^2x is equal to tan^2x because tangent is opposite over adjacent (y/x). For the easy one, we know that anything over itself is 1 so cos^2x/cos^2x is 1 and then lastly we know that 1/cos^2x is the same thing as saying sec^2x. We simply are plugging in until it simplifies nicely. To conclude we have tan^2x+1=sec^2x. Yay! 

    To derive the identity with Co-secant and Cotangent we would start with the same original one, but divide by sin^2x. We know that after doing so the sines will equal 1 and cos^2x over sin^2x is the same thing as saying cot^2x so we would have 1+cot^2x= ...csc^2x since 1/sin^2x is csc^2x. 

    In order to see what is going on the picture below will hopefully help. 

 

Inquiry Activity Reflection: 

1. "The connection that I see between units N, O, P, and Q so far is...that everything in some sort of way comes together to conclude and involve the unit circle and triangles are involved as well. 

2. "If I had to describe trigonometry in 3 words, they would be...ratios, substitutions, and strangely comprehensible. 

WPP#13&14: Unit P Concept 6&7

"Please see my WPP13-14, made in collaboration with Jesus H., by visiting his blog jesushperiod5.blogspot.com.  Also be sure to check out the other awesome posts on his blog."

BQ#1: Unit P Concept 1 and 4 Law of Sines and the Area of an Oblique Triangle

i. Law of Sines 

Why do we need it?

Well, in the past we have been working with all right triangles and it was rather easy when we had to find an angle or a side length due to the fact that we would use SOH CAH TOA (Sine, Cosine, or Tangent), or we would use the Pythagorean Theorem (a^2+b^2=c^2). However, what do we do when it comes to non-right triangles? Hmm..well the law of sines isn't just there for no reason. We can use the Law of Sines to figure out what an angle or side off a triangle is. The law of sines formula is the following: 

                                                                         http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif

      
    http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpg
                                                                   

How is it derived?

Okay so having a regular triangle in front of us, we would draw a vertical line form angle C down to the side length ab making two triangles now and we can label that with an "h" since it is the height. The height will belong to both triangles and a right triangle will be made. Yay! Right triangles are easier to work with right? The bottom picture will give  you a visual so you can see how it's done and for further help. 

 http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif

Now, we know that the formula for the area of a triangle is A= 1/2 Base x Height, yet we can change it up depending on what we are looking for and it can still mean the same thing. That's the beauty of math! So, if we are trying to find h and we know that sinA= h/c and in order to find h we can say h= csinA by simply multiplying c to both sides. Same as if we were using sinC, sinC=h/a and in order to find h we would multiply a to both sides and we would end with a result looking like this, h=asinC. It does become a bit easier now because we are aware that these expressions are both equaled to h so can we not just equal them to each other? Yes! Therefore, we would have csinA=asinC. Are we done? No because well the formula doesn't look it should as stated above. One more step! To get sinA and sinC alone on the top we will divide by ac and then we would have SinA/a=SinC/c. You might ask yourself what about the B, but in reality it is the same thing. If we would have used angle B instead of C we should have SinA/a=SinB/b. We can see that they are all equal to each other and so the order does not matter. And that is how the formula is as is and came to be. The following images will help a bit more and you shall see what is going on. 

  

iv. Area Formula (Oblique Formula) 

In order to find the area of a triangle we use the formula A=1/2bh and this would certainly work out if all triangles were right triangles, but since life isn't always nice and sweet we will get triangles of which are not right and we have to be able to find h, the height. 

We would begin by doing the same thing as before and cutting the triangle into two by drawing the vertical line. Since we do not know what h is what can we do? Well, we do know that h=aSinC like we discovered up above first, so we can substitute. A=1/2b(aSinC). Now, we can use more than one depending on what angles and stuff. For example we could use 1/2 bc SinA; 1/2 ac SinB; 1/2 ab SinC. 

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp

References:

 http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif  http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif

 http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpghttps://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp

   

WPP #12: Unit O Concept 10: Solving angles of elevation and depression word problems

A) Sophia is tired of the same routine and so she decides to go up to the mountains with Edward and more friends. She is excited and thrilled about the whole trip up to Big Bear and she is hoping to have a blast with everyone. Now, as soon as they get there, Edward suggests going skiing and everyone says yes. As Sophia gets ready and then puts her skis on at the bottom of the mountain, she stands 700 feet away from it, she finds that the angle of elevation is 15 degrees. Before actually going up the mountain and then having a blast coming down, Sophia wants to know how high the mountain is. Estimate the height of the mountain and round to the nearest foot. 

B) So, after a while Sophie and Edward were the first ones to make it to the top of the mountain and they decide to contemplate the view from up top and they enjoy themselves for a while before racing down. As Sophia gets ready to ski down she stands at the tip of it and looks down. She estimates the angle of depression to be 25 degrees from where she is at the top to the very bottom of the mountain where all of her other friends were. Also, she is aware that the height of which she is found in now is 850 feet. How far down is the path that she will ski down? Round to the nearest foot. 

Answers: 

Cites for the 2 pictures I got on Google: 

http://www.disneyclips.com/imagesnewb/imageslwrakr01/pooh_tigger_piglet_eeyore_skis.gif

https://www.google.com/search?tbm=isch&tbs=simg:CAQSWxpZCxCo1NgEGgIICQwLELCMpwgaMgowCAESCqQEqQSsBKMEqAQaIKKoJxY7wJjGpCP8yYxW5LjlhGuMA5uFdfg5i9pv13V4DAsQjq7-CBoKCggIARIEasBVogw&sa=X&ei=vQ4YU7z2MZL9oATJm4EQ&ved=0CCMQwg4oAA&biw=1366&bih=667#facrc=_&imgdii=_&imgrc=rmBk_ghzxFEHvM%253A%3BAjyJcOxxAv9kwM%3Bhttp%253A%252F%252Fimg1.etsystatic.com%252F024%252F0%252F8427078%252Fil_340x270.490026831_a8ds.jpg%3Bhttp%253A%252F%252Fwww.etsy.com%252Fmarket%252Ffrozen_lake%3B340%3B270

I/D #2: Unit O Concept 7-8: Deriving the patterns for the 45-45-90 and 30-60-90 Triangles

Inquiry Activity Summary:

Today in  class we were given a square and an equilateral triangle both having a side length of 1 and we were to explain the thought process step by step in order to be able and literally know how and why the special right triangles have their constants and basically where they come from. Now, for the 45-45-90 triangle we were given the square that had a length of 1 while for the 30-60-90 triangle we were given the equilateral triangle with a length of 1 and from there we were to completely derive it and see how you get n, n, n radical 2 for the 45 degree one and n, n radical 3, and 2n. Okay so although it seems like we know nothing and we feel like we cannot figure out..we can step by step.

1. Okay so beginning with the square that we were given for the 45 degree special triangle, we can automatically label all four sides with a 1 since we know that a square is all equal in sides and the directions did say that the square contained a side length of 1. Now, we can bisect the square diagonally of course because if we did it vertically it will not create a triangle, but a rectangle. Then, it only gets easier and this is why, we know that two sides are equaled to 1 and  so in order to find the third side we can use the wonderful ...PYTHAGOREAN THEOREM! After solving it by using a^2+b^2=c^2 we should get c= radical 2. Okay now I know what you are thinking well then where does the n come from and well truth is n is just used as a constant it really isn't anything else but a constant/variable like x could be. So we could label all three sides of the right triangle as n like any variable and then we find that the sides conclude to being n, n, and n radical 2. The reason we use n is to that we can see the relationship with all sides and so we can see the possible numbers that could be interchangeable. There is a visual below so that it can be easier in understanding and seeing a picture may clear confusions.

 

2. Okay so now for the 30-60-90 triangle we are given an equilateral triangle of which we all know has three angles that are 60 degrees. We can begin by labeling the three sides with one since the directions as well told us that there was a side length equal to 1. In order to have it become a right triangle we simply bisect it vertically and the reason is considering that we will get a 90 degree, a 30, and a 60 degree like shown below. By cutting it so, it basically creates out special triangle with the wanted angles. Now, by just focusing on the triangle we want we can see that the bottom becomes 1/2 after bisecting it, while the hypotenuse still is 1, and now what about the height? Well, we can use the Pythagorean Theorem again and after plugging in and solving, we should get b= radical 3/2. Okay so now we have 1, radical 3/2, and 1/2, yet we are not done. After, we can do some more solving by multiplying by 2. This is so because well 1/2 times 2 gives us one and that is what we originally had, yet now we have to do it to all sides. Next, once we multiply we should get 2 for the hypotenuse, 1 for the bottom horizontal line and lastly radical 3 for the height. Now, almost finishing, where the heck does the n mean and why does it fit in? Well, n is just a constant of which we use to compare the sides and it basically represents the different number values. Now, after we label all sides with the n as simply a variable we end up getting n, n radical 3, and 2n. The figures below help much visually when it comes to understanding.

Inquiry Activity Reflection:

1. "Something I never noticed before about special right triangles is that they can appear and simply pop out of no where and especially out of other shapes."

2. "Being able to derive these patterns myself aids in my learning because I can actually see what I am learning and exactly where this comes from that this didn't just appear form thin air." 

I/D#1:Unit N Concept 7: How do RST relate to the UC?

Inquiry Activity Summary:

1. 30 degrees 

Several different instructions were given in order to complete this special right triangle of 30 degrees and much labeling in order to understand. To start with, the three sides of the triangle had to be labeled for their identification. So, one thing we know for sure and that is that our hypotenuse is equaled to 1 considering that these triangles all come from within a unit circle and what is a unit circle? Well a unit circle is one of which has a radius of one and therefore, we can see how the longer side (hypotenuse) is that radius of the circle. Now, according to the special rules of right triangles we know that the side adjacent to the 30 degrees (form the picture it is the horizontal side labeled x) will be n radical 3. Also, we find out that the side opposite from the 30 degrees (due to the picture it is the vertical side labeled y) will be n and finally we get to the hypotenuse (r) of which is said to be 2n. Okay now that that is over with, we can actually find real number values and that is done by using two trig functions: Sine and Cosine. Sine of 30 degrees is done by using SOH and therefore will be opposite over hypotenuse; we can write it out as y/r or x/2x of which equals 1/2 once it is simplified. Doing the same thing with cosine but this time using CAH, adjacent over hypotenuse, it would be x/r and with the variables it would be radical 3/2 after the simplifying like shown in the image above. If we were to treat the triangle on a coordinate plane with the origin of the 30 degrees being (0,0) then the corner as you move horizontally will be (radical 3/2,0) and lastly, the point at the highest tip will be (radical 3/2, 1/2).

2. 45 degrees

Now the same types of instructions apply to this 45 degree triangle, yet the numbers will be different. Okay so to start we can label the adjacent side, the horizontal side of the given angle on the left hand corner x. The opposite side of the angle or the vertical side will be labeled as y and lastly for now the hypotenuse will be r=1. To label according to STR, both x and y will be n, and as for the hypotenuse is will be n radical 2 after simplifying of course like shown in the image. The trig functions world the same as last time with sine and cosine. Sine and cosine are actually the same number values and they both include the same type of simplification since for both the x and y it is n/n radical 2 of which reduces to radical 2 over 2. From my perspective this special triangle is the easiest and includes less work. Picturing the image on a coordinate plane, the origin will be (0,0) and as you move horizontally across then the next point will be (radical 2/2, 0) and then as for the last vertical tip point it will be (radical 2/2, radical 2/2).  

3. 60 degrees

Okay so we are finally looking at the last type of triangle! Yay! We shall label the horizontal and vertical and hypotenuse like the same as the others, with x, y, and r=1. X is the adjacent and y is the opposite one. Considering the special rules, x will be n and y will be n radical 3. To find sine of 60 degrees then it will be y/r and then to find actual values it will turn into radical 3 over 2. Also, for cosine it will be x/r and then 1/2 after the simplification as shown. Treating the triangle as if on a coordinate plane starting as the origin (0,0) and then as you keep going across horizontally the point will become (1/2,0). Lastly, the last point will be (1/2,radical 3/2). 

4. This activity helps derive the unit circle by being able to see special right triangles from within the circle. We can see how the SOH CAH TOA can develop and we can see the different types of degrees within it.

5.

Depending on which quadrant the SRT is found, that will be the determination on whether it will be positive or negative. If it will be found on quadrant one then both x and y will be positive; if it is then in quadrant 2 then only the x value will be negative while the y is positive. Also, the third quadrant both x and y are negative. Lastly, for quadrant 4 then only the y value is negative. 

1. The coolest thing I have learned from this activity was...that the unit circle actually does include the special right triangles and how a lot can come from a simple circle. 

2. This activity will help me in this unit because ... I will not have to literally memorize the entire unit circle.

3. Something I never realized before about special right triangles and the unit circle is... how they can come together and actually make sense. I would've never thought so much could be learned. 

RWA #1: Unit M Concept 5: Ellipses

1. Definition: the set of all points such that the sum of the distance from 2 points, known as the foci, is a constant.
2. Properties: The equation of an ellipse looks like this and it has a bit more information below:

To describe it graphically, an ellipse has a sort of oval type shape and it can either be skinny or a fat one. The ellipse has a major and a minor axis, followed by a center and then there is also a foci of which lies inside within the ellipse. The following image shows an example of a horizontal and vertical ellipse:

  

For more information on ellipses go to:   http://www.purplemath.com/modules/ellipse.htm

 All of the features of an ellipse involve the center of which is made up of (h,k) and then finding the vertices and the co-vertices. Now, to do so you take the square root of the value of a and then adding or subtracting it to the h or k depending on whether it's major axis is vertical or horizontal. The co-vertices you can find likewise just that you would use b and then add or subtract. The foci comes in next and it dictates where the foci is going to be and it tells whether the ellipse will be horizontal or vertical. Lastly, for the eccentricity of the ellipse, it will always be greater than 0 but less than one. Below will be a video of which will tell how you can solve an ellipse and it contains extra help on the graphing as well:

3. The Real World Application: 
The solar system is an example of ellipses. They discovered that the planets travel around the sun from one of its foci. To see the example and actually view and have this real world application explained then view the video below.



4. The Works Cited
http://www.youtube.com/watch?v=48tXquj94w8

http://www.purplemath.com/modules/ellipse.htm

http://www.youtube.com/watch?v=9xSgKqTxZbg

https://www.google.com/search?hl=en&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=ellipse+equation&oq=ellipse+&gs_l=img.3.0.0l10.8705.9953.0.14344.8.8.0.0.0.0.110.724.3j5.8.0....0...1ac.1.34.img..1.7.620.M5FepgyTgVw#hl=en&q=horizontal+and+vertical+ellipsis&spell=1&tbm=isch&imgdii=_

https://www.google.com/search?hl=en&site=imghp&tbm=isch&source=hp&biw=1366&bih=667&q=ellipse+equation&oq=ellipse+&gs_l=img.3.0.0l10.8705.9953.0.14344.8.8.0.0.0.0.110.724.3j5.8.0....0...1ac.1.34.img..1.7.620.M5FepgyTgVw#hl=en&q=ellipses+equation&tbm=isch&facrc=_&imgdii=_&imgrc=FBWW2sN-ezU7hM%253A%3BIgSAy7XveaBvgM%3Bhttp%253A%252F%252Fwww.descarta2d.com%252FBookHTML%252FChapters%252FHTMLFiles%252Fell_32.gif%3Bhttp%253A%252F%252Fwww.descarta2d.com%252FBookHTML%252FChapters%252Fell.html%3B346%3B233