i. Law of Sines
Why do we need it?
Well, in the past we have been working with all right triangles and it was rather easy when we had to find an angle or a side length due to the fact that we would use SOH CAH TOA (Sine, Cosine, or Tangent), or we would use the Pythagorean Theorem (a^2+b^2=c^2). However, what do we do when it comes to non-right triangles? Hmm..well the law of sines isn't just there for no reason. We can use the Law of Sines to figure out what an angle or side off a triangle is. The law of sines formula is the following:
http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif
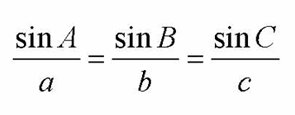
http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpg
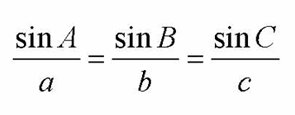

http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpg
How is it derived?
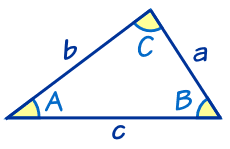
Okay so having a regular triangle in front of us, we would draw a vertical line form angle C down to the side length ab making two triangles now and we can label that with an "h" since it is the height. The height will belong to both triangles and a right triangle will be made. Yay! Right triangles are easier to work with right? The bottom picture will give you a visual so you can see how it's done and for further help.

http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif
Now, we know that the formula for the area of a triangle is A= 1/2 Base x Height, yet we can change it up depending on what we are looking for and it can still mean the same thing. That's the beauty of math! So, if we are trying to find h and we know that sinA= h/c and in order to find h we can say h= csinA by simply multiplying c to both sides. Same as if we were using sinC, sinC=h/a and in order to find h we would multiply a to both sides and we would end with a result looking like this, h=asinC. It does become a bit easier now because we are aware that these expressions are both equaled to h so can we not just equal them to each other? Yes! Therefore, we would have csinA=asinC. Are we done? No because well the formula doesn't look it should as stated above. One more step! To get sinA and sinC alone on the top we will divide by ac and then we would have SinA/a=SinC/c. You might ask yourself what about the B, but in reality it is the same thing. If we would have used angle B instead of C we should have SinA/a=SinB/b. We can see that they are all equal to each other and so the order does not matter. And that is how the formula is as is and came to be. The following images will help a bit more and you shall see what is going on.
iv. Area Formula (Oblique Formula)
In order to find the area of a triangle we use the formula A=1/2bh and this would certainly work out if all triangles were right triangles, but since life isn't always nice and sweet we will get triangles of which are not right and we have to be able to find h, the height.
We would begin by doing the same thing as before and cutting the triangle into two by drawing the vertical line. Since we do not know what h is what can we do? Well, we do know that h=aSinC like we discovered up above first, so we can substitute. A=1/2b(aSinC). Now, we can use more than one depending on what angles and stuff. For example we could use 1/2 bc SinA; 1/2 ac SinB; 1/2 ab SinC.

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp
References:
http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif
http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpghttps://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp


No comments:
Post a Comment