SP#7: Unit Q Concept 2: Finding all trig functions when given one trig function and quadrant (using identities)

"This SP#7 was made in collaboration with Tracey P. Please visit the other awesome posts on their blog by going here."

Now, there is more than one way to find our answers and solve for the function, two are those that will be expressed throughout this post. We know that we can solve this using identities or by using SOH CAH TOA! So, the following pictures will display the solutions to the problems in both ways and using both methods. (: In the end we will find out how you get the same answers either way!

The first image will show and go over how to solve this function when using identities.

This second image will go over solving the function by using the wonderful SOH CAH TOA!  

In order to be able and understand this problem and be able to deal with it as you solve it, you have to be able to know the different types of identities and they should be able to mix and match and substitute several terms for others. Also, of course you have to know what SOH CAH TOA is and the ratios for each. Also, you should be familiar with all of the ratios and how there could be more than one. It can be difficult, but with practice everything will be fine. (:  

I/D#3: Unit Q Concept 1: Pythagorean Identities

Inquiry Activity Summary:
1. Okay so we know that we are dealing with identities because the title is a given, yet what are identities? Well, an identity is basically any proven fact or formula of which brings the Pythagorean Theorem to mind considering that it is a formula that works and is always correct when put to use. Okay so let's start off with the Pythagorean Theorem. If we were given the terms x, y, and r then we would write out the formula like this: x^2+y^2=r^2, but we would tweak it a bit in order to have it equal to 1. We would divide by r^2, do we agree? Yes! Because that is pretty much the only way to equal an equation to 1, by dividing by whatever number the equation is equaled to. Then we would have (x/r)^2+(y/r)^2=1.
 
     Now, if we go back to the unit circle, oh yeah I forgot to mention that the unit circle does come back to haunt haha, we know that cosine is x/r or in other words, adjacent over hypotenuse and sine is y/r or opposite over hypotenuse, so ..do we see anything? Hmm.. Yea! It matches to much of the Pythagorean Theorem! We would just have to square the two variables on the left, x and y, and then equal them to 1. In the end we could have cos^2theta + sin^2theta= 1. Remember that cosine is x and sin is y so in reality we just do some switching around and have fun with it and therefore sin^2x+cos^2x=1 is referred to as a Pythagorean Identity. To prove the theory with some examples and so you can see it visually look at the images below if let's say we did the magic 45 degree.

2. Now, to derive the identity with Secant and Tangent we would start off with the original sin^2x+cos^2x=1. The first thing we would do is divide everything by cos^2x and we would get sin^2x/cos^2x + cos^2x/cos^2x= 1/cps^2x and we can still simplify this further! We know that sin^2x/cos^2x is equal to tan^2x because tangent is opposite over adjacent (y/x). For the easy one, we know that anything over itself is 1 so cos^2x/cos^2x is 1 and then lastly we know that 1/cos^2x is the same thing as saying sec^2x. We simply are plugging in until it simplifies nicely. To conclude we have tan^2x+1=sec^2x. Yay! 

    To derive the identity with Co-secant and Cotangent we would start with the same original one, but divide by sin^2x. We know that after doing so the sines will equal 1 and cos^2x over sin^2x is the same thing as saying cot^2x so we would have 1+cot^2x= ...csc^2x since 1/sin^2x is csc^2x. 

    In order to see what is going on the picture below will hopefully help. 

 

Inquiry Activity Reflection: 

1. "The connection that I see between units N, O, P, and Q so far is...that everything in some sort of way comes together to conclude and involve the unit circle and triangles are involved as well. 

2. "If I had to describe trigonometry in 3 words, they would be...ratios, substitutions, and strangely comprehensible. 

WPP#13&14: Unit P Concept 6&7

"Please see my WPP13-14, made in collaboration with Jesus H., by visiting his blog jesushperiod5.blogspot.com.  Also be sure to check out the other awesome posts on his blog."

BQ#1: Unit P Concept 1 and 4 Law of Sines and the Area of an Oblique Triangle

i. Law of Sines 

Why do we need it?

Well, in the past we have been working with all right triangles and it was rather easy when we had to find an angle or a side length due to the fact that we would use SOH CAH TOA (Sine, Cosine, or Tangent), or we would use the Pythagorean Theorem (a^2+b^2=c^2). However, what do we do when it comes to non-right triangles? Hmm..well the law of sines isn't just there for no reason. We can use the Law of Sines to figure out what an angle or side off a triangle is. The law of sines formula is the following: 

                                                                         http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif

      
    http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpg
                                                                   

How is it derived?

Okay so having a regular triangle in front of us, we would draw a vertical line form angle C down to the side length ab making two triangles now and we can label that with an "h" since it is the height. The height will belong to both triangles and a right triangle will be made. Yay! Right triangles are easier to work with right? The bottom picture will give  you a visual so you can see how it's done and for further help. 

 http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif

Now, we know that the formula for the area of a triangle is A= 1/2 Base x Height, yet we can change it up depending on what we are looking for and it can still mean the same thing. That's the beauty of math! So, if we are trying to find h and we know that sinA= h/c and in order to find h we can say h= csinA by simply multiplying c to both sides. Same as if we were using sinC, sinC=h/a and in order to find h we would multiply a to both sides and we would end with a result looking like this, h=asinC. It does become a bit easier now because we are aware that these expressions are both equaled to h so can we not just equal them to each other? Yes! Therefore, we would have csinA=asinC. Are we done? No because well the formula doesn't look it should as stated above. One more step! To get sinA and sinC alone on the top we will divide by ac and then we would have SinA/a=SinC/c. You might ask yourself what about the B, but in reality it is the same thing. If we would have used angle B instead of C we should have SinA/a=SinB/b. We can see that they are all equal to each other and so the order does not matter. And that is how the formula is as is and came to be. The following images will help a bit more and you shall see what is going on. 

  

iv. Area Formula (Oblique Formula) 

In order to find the area of a triangle we use the formula A=1/2bh and this would certainly work out if all triangles were right triangles, but since life isn't always nice and sweet we will get triangles of which are not right and we have to be able to find h, the height. 

We would begin by doing the same thing as before and cutting the triangle into two by drawing the vertical line. Since we do not know what h is what can we do? Well, we do know that h=aSinC like we discovered up above first, so we can substitute. A=1/2b(aSinC). Now, we can use more than one depending on what angles and stuff. For example we could use 1/2 bc SinA; 1/2 ac SinB; 1/2 ab SinC. 

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp

References:

 http://www.regentsprep.org/Regents/math/algtrig/ATT12/sineprooof.gif  http://www.mathsisfun.com/algebra/images/trig-sine-rule.gif

 http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas_files/image033.jpghttps://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhiF0XgXcK6W-1OZJJFzreG2EGOLWW_zDEN9WhU24uWq9gr1RV5YK5_VKuLU0yvzkTJXcJRTCxZ97Z39QI3jryus7qSobkNg7ZVsl9S3JoN86vHz9Nzd67G94-r34GfRgt7bfJ2FcBbWRc/s400/hi.bmp

   

WPP #12: Unit O Concept 10: Solving angles of elevation and depression word problems

A) Sophia is tired of the same routine and so she decides to go up to the mountains with Edward and more friends. She is excited and thrilled about the whole trip up to Big Bear and she is hoping to have a blast with everyone. Now, as soon as they get there, Edward suggests going skiing and everyone says yes. As Sophia gets ready and then puts her skis on at the bottom of the mountain, she stands 700 feet away from it, she finds that the angle of elevation is 15 degrees. Before actually going up the mountain and then having a blast coming down, Sophia wants to know how high the mountain is. Estimate the height of the mountain and round to the nearest foot. 

B) So, after a while Sophie and Edward were the first ones to make it to the top of the mountain and they decide to contemplate the view from up top and they enjoy themselves for a while before racing down. As Sophia gets ready to ski down she stands at the tip of it and looks down. She estimates the angle of depression to be 25 degrees from where she is at the top to the very bottom of the mountain where all of her other friends were. Also, she is aware that the height of which she is found in now is 850 feet. How far down is the path that she will ski down? Round to the nearest foot. 

Answers: 

Cites for the 2 pictures I got on Google: 

http://www.disneyclips.com/imagesnewb/imageslwrakr01/pooh_tigger_piglet_eeyore_skis.gif

https://www.google.com/search?tbm=isch&tbs=simg:CAQSWxpZCxCo1NgEGgIICQwLELCMpwgaMgowCAESCqQEqQSsBKMEqAQaIKKoJxY7wJjGpCP8yYxW5LjlhGuMA5uFdfg5i9pv13V4DAsQjq7-CBoKCggIARIEasBVogw&sa=X&ei=vQ4YU7z2MZL9oATJm4EQ&ved=0CCMQwg4oAA&biw=1366&bih=667#facrc=_&imgdii=_&imgrc=rmBk_ghzxFEHvM%253A%3BAjyJcOxxAv9kwM%3Bhttp%253A%252F%252Fimg1.etsystatic.com%252F024%252F0%252F8427078%252Fil_340x270.490026831_a8ds.jpg%3Bhttp%253A%252F%252Fwww.etsy.com%252Fmarket%252Ffrozen_lake%3B340%3B270

I/D #2: Unit O Concept 7-8: Deriving the patterns for the 45-45-90 and 30-60-90 Triangles

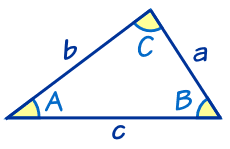
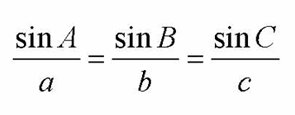Inquiry Activity Summary:

Today in  class we were given a square and an equilateral triangle both having a side length of 1 and we were to explain the thought process step by step in order to be able and literally know how and why the special right triangles have their constants and basically where they come from. Now, for the 45-45-90 triangle we were given the square that had a length of 1 while for the 30-60-90 triangle we were given the equilateral triangle with a length of 1 and from there we were to completely derive it and see how you get n, n, n radical 2 for the 45 degree one and n, n radical 3, and 2n. Okay so although it seems like we know nothing and we feel like we cannot figure out..we can step by step.

1. Okay so beginning with the square that we were given for the 45 degree special triangle, we can automatically label all four sides with a 1 since we know that a square is all equal in sides and the directions did say that the square contained a side length of 1. Now, we can bisect the square diagonally of course because if we did it vertically it will not create a triangle, but a rectangle. Then, it only gets easier and this is why, we know that two sides are equaled to 1 and  so in order to find the third side we can use the wonderful ...PYTHAGOREAN THEOREM! After solving it by using a^2+b^2=c^2 we should get c= radical 2. Okay now I know what you are thinking well then where does the n come from and well truth is n is just used as a constant it really isn't anything else but a constant/variable like x could be. So we could label all three sides of the right triangle as n like any variable and then we find that the sides conclude to being n, n, and n radical 2. The reason we use n is to that we can see the relationship with all sides and so we can see the possible numbers that could be interchangeable. There is a visual below so that it can be easier in understanding and seeing a picture may clear confusions.

 

2. Okay so now for the 30-60-90 triangle we are given an equilateral triangle of which we all know has three angles that are 60 degrees. We can begin by labeling the three sides with one since the directions as well told us that there was a side length equal to 1. In order to have it become a right triangle we simply bisect it vertically and the reason is considering that we will get a 90 degree, a 30, and a 60 degree like shown below. By cutting it so, it basically creates out special triangle with the wanted angles. Now, by just focusing on the triangle we want we can see that the bottom becomes 1/2 after bisecting it, while the hypotenuse still is 1, and now what about the height? Well, we can use the Pythagorean Theorem again and after plugging in and solving, we should get b= radical 3/2. Okay so now we have 1, radical 3/2, and 1/2, yet we are not done. After, we can do some more solving by multiplying by 2. This is so because well 1/2 times 2 gives us one and that is what we originally had, yet now we have to do it to all sides. Next, once we multiply we should get 2 for the hypotenuse, 1 for the bottom horizontal line and lastly radical 3 for the height. Now, almost finishing, where the heck does the n mean and why does it fit in? Well, n is just a constant of which we use to compare the sides and it basically represents the different number values. Now, after we label all sides with the n as simply a variable we end up getting n, n radical 3, and 2n. The figures below help much visually when it comes to understanding.

Inquiry Activity Reflection:

1. "Something I never noticed before about special right triangles is that they can appear and simply pop out of no where and especially out of other shapes."

2. "Being able to derive these patterns myself aids in my learning because I can actually see what I am learning and exactly where this comes from that this didn't just appear form thin air."